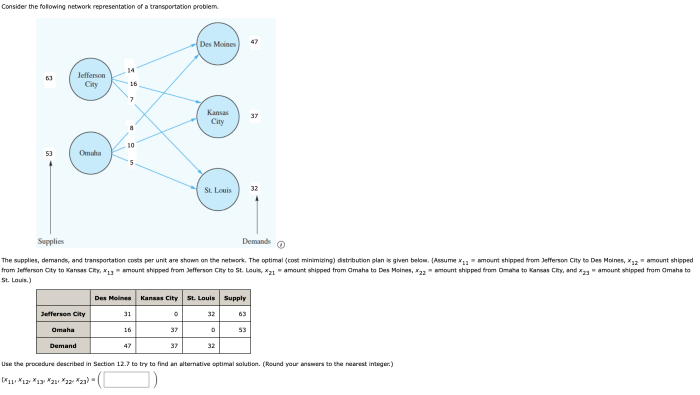
Consider the following network representation of a transportation problem: a diagrammatic portrayal of a transportation network, illustrating its nodes, arcs, and capacities, effectively representing the problem’s complexities. This network representation serves as a valuable tool for analyzing and solving transportation problems, offering advantages and disadvantages that shape its utility in practice.

The network representation of a transportation problem provides a structured framework for understanding the problem’s elements and their interrelationships. Nodes represent locations, while arcs represent the routes connecting them. Capacities indicate the maximum flow that can be transported along each arc.

This representation enables the application of mathematical techniques to analyze the problem, such as linear programming and network flow algorithms.

Network Representation of a Transportation Problem

A transportation problem is a mathematical optimization problem that deals with the distribution of goods from multiple sources to multiple destinations at minimum cost. A network representation of a transportation problem is a graphical representation of the problem that helps visualize and analyze the problem.

The network consists of nodes and arcs. Nodes represent the sources and destinations, while arcs represent the possible routes between the nodes. Each arc has a capacity, which represents the maximum amount of goods that can be transported along that route.

The objective of the transportation problem is to determine the optimal flow of goods from the sources to the destinations such that the total transportation cost is minimized.

Analysis of the Network Representation

The network representation of a transportation problem can be used to analyze the problem in several ways.

• It can be used to identify the critical paths in the network, which are the paths that have the greatest impact on the total transportation cost.
• It can be used to identify the bottlenecks in the network, which are the points where the flow of goods is restricted.
• It can be used to evaluate the sensitivity of the solution to changes in the input data, such as the demand at the destinations or the capacity of the arcs.

The network representation can also be used to solve the transportation problem using a variety of optimization techniques, such as linear programming or network flow algorithms.

Methods for Solving Transportation Problems

There are a variety of methods that can be used to solve transportation problems.

• The northwest corner method is a simple and intuitive method that starts by assigning the maximum possible amount of goods to the northwest corner cell of the transportation table.
• The Vogel’s approximation method is a more sophisticated method that takes into account the transportation costs when assigning goods to the cells of the transportation table.
• The linear programming method is a general-purpose optimization technique that can be used to solve transportation problems of any size.

The choice of which method to use depends on the size and complexity of the transportation problem.

Applications of Network Representations in Transportation: Consider The Following Network Representation Of A Transportation Problem:

Network representations are used in a variety of applications in transportation, including:

• Transportation planning:Network representations can be used to model and analyze transportation systems, such as road networks or public transit systems.
• Traffic management:Network representations can be used to monitor and manage traffic flow in real time.
• Logistics:Network representations can be used to optimize the distribution of goods and services.

Network representations are a powerful tool for analyzing and solving transportation problems.

FAQ Summary

What is the purpose of a network representation in a transportation problem?

A network representation provides a structured framework for visualizing and analyzing a transportation problem, enabling the application of mathematical techniques for optimization.

What are the advantages of using a network representation?

Advantages include the ability to simplify the problem structure, visualize the problem, and apply mathematical techniques for optimization.

What are the limitations of using a network representation?

Limitations may include the inability to capture certain aspects of real-world transportation problems, such as stochastic demand and time-dependent travel times.